Estimating proton heating related with turbulence in the solar wind by means of high-resolution hybrid simulations

Although turbulence is generally driven by violent events or instabilities at large scales, a further cascade is responsible for transferring energy via nonlinear coupling from the large injection scale to much smaller scales, through the ion and the electron characteristic regimes, where they are eventually dissipated. The estimated turbulent energy cascade rate is comparable to the proton heating needed to explain the non-adiabatic evolution of the solar wind plasma during its expansion. This suggests that turbulence plays an active role in transferring energy from electromagnetic fields to particles and heats the solar wind plasma. However, the processes that ultimately lead to heating in a collisionless turbulent medium are still unknown.
 
By performing high-resolution 2D numerical simulations with the CAMELIA code, we were able to investigate the evolution of the parallel and perpendicular proton temperatures during the development of a turbulent activity.
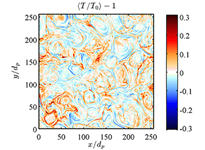
As a result of the interaction of particles with the turbulent fluctuations and small-scale structures, we observe an overall parallel and perpendicular heating with similar rates, so that the temperature of the plasma remains globally nearly isotropic. However, the absence of a global preferential heating does not imply the absence of signatures of localized preferential deformations of the particle distribution functions. Indeed, we observe strong local temperature anisotropies, which seem to be concentrated in regions with stronger coherent structures, identified by the presence of current sheets [Fig. 1]. These results are in agreement with previous works based on the Vlasov-hybrid approximation. As the overall heating is rather weak, slow, and nearly isotropic, we can infer that the local formation of large proton temperature anisotropies is likely due to energy exchanges between the parallel and perpendicular directions, and/or to the spatial transport, rather than due to the heating.
 
A very important point to mention is that the parallel proton heating is found to be independent on the chosen value for the resistivity coefficient, the number of particles and the spatial resolution employed, while the perpendicular proton temperature strongly depends on these parameters [Fig. 2]. If too few particles are employed, or if the resistivity is too low, the perpendicular heating can be largely overestimated/unphysical. Conversely, when a too strong value of the resistivity is implemented, the artificial damping of fluctuations at ion scales can produce a strong reduction of the perpendicular heating, thus generating an equally unphysical preferential parallel heating. This proves that no firm conclusions can be drawn about the perpendicular heating by turbulence in hybrid simulations, unless a careful and empirically fine-tuned choice of all parameters has been taken.
 

Figure 1. Contour plots of four different quantities on the simulation plane at the time of maximum turbulent activity: the amplitude of the in-plane magnetic fluctuations (upper left panel),  the out-of-plane current density (upper right panel), the proton temperature anisotropy A_p=T_p⊥/T_p∥ (bottom left panel), and the proton temperature variation normalized to the initial temperature (bottom right panel).


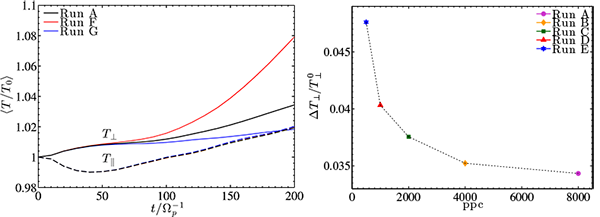Figure 2. Left panel: time evolution of the parallel and perpendicular proton temperature, T_∥ and T_⊥, respectively, normalized to the initial common value, T₀. The evolution is here shown for different values of the resistive coefficient. Right panel: Perpendicular proton heating, computed at the time of maximum turbulent activity, vs. the number of particles-per-cell (ppc) employed, ranging from 8000 to 500.

References
 
Franci L., Landi S., Matteini L., Verdini A., and Hellinger P., ApJ 812:1 (2015)
“High-resolution hybrid simulations of kinetic turbulence at proton scales”
Link: adsabs.harvard.edu/abs/2015ApJ...812...21F
 
CAMELIA code’s website
terezka.asu.cas.cz/helinger/camelia.html